Основы работы с TensorFlow и Keras на Python. Часть 2
В предыдущей статье были описаны основы работы с Tensorflow и Keras API на Python. Эта статья посвящена задаче бинарной классификации — возможно, одной из самых частых задач машинного обучения. Задача бинарной классификации будет рассматриваться на примере набора данных IMDB dataset. Необходимо отнести рецензию о фильме к положительной или отрицательной по используемым в рецензии словам. Набор данных разделён на обучающую и тестовую выборки. Половина отзывов положительные, половина отрицательные.
Для начала, загрузим IMDB dataset:
from keras.datasets import imdb (train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
num_words=10000 означает, что мы возьмём 10000 наиболее часто встречающихся в рецензиях слов.
Переменные train_data и test_data - списки рецензий. Каждая рецензия представляет собой индексы (номера) слов из словаря.
train_labels и test_labels - списки 0 и 1, где 0 означает отрицательный, а 1 - положительный отзыв.
Например,
print (train_data[10]) [1, 785, ..., 2068, 545]
Означает, что рецензия №10 из обучающей выборки train_data состоит из слов с номерами 1, 785, ..., 2068, 545 А сам отзыв №10 является положительным
print (train_labels[10]) 1
Если необходимо получить само слово (на английском языке), необходимо сделать следующее:
word_index = imdb.get_word_index() word_index = dict([(key, value + 3) for (key, value) in word_index.items()]) reverse_word_index = dict([(value, key) for (key, value) in word_index.items()]) decoded_review = ' '.join([reverse_word_index.get(i, '?') for i in train_data[10]]) print (decoded_review)
Это выведет все слова из рецензии 10:
? french horror cinema has seen something of a revival over the last couple of years...
И если ввести эти слова в поисковик, мы получим ссылку на фильм Maléfique (2002).
Подготовка данных
Мы не можем передать нейронной сети просто список целых чисел. Их необходимо преобразовать в тензоры. Есть два способа сделать это:
1.Разметить списки так, чтобы все они имели одну длину, затем преобразовать список в тензор с формой (samples, word_indeces). Потом сделать первый слой в сети таким, чтобы он принимал на вход целочисленные тензоры.
2. Преобразовать списки целых чисел в векторы 0 и 1. Это будет означать, к примеру, преобразование списка [3, 5] в 10000-мерный вектор, почти весь состоящий из 0, за исключением индексов 3 и 5, которые будут хранить значение 1. Далее можно использовать полносвязный слой Dense, который умеет работать с числами с плавающей запятой в виде вектора.
Используем вариант 2. Закодируем последовательности целых чисел в бинарную матрицу:
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return results
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
После кодирования исходные данные выглядят так:
>>> x_train[0] array([ 0., 1., 1., ..., 0., 0., 0.])
Так же векторизуем выходные значения (ответы):
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
Теперь данные подготовлены для нейронной сети.
Построение сети
Входные данные — это векторы, выходные данные (ответы) — это скаляры (0 и 1). Сеть, которая хорошо решает задачу бинарной классификации, — это простой набор полносвязных слоёв с функцией активации relu: Dense(16,activation='relu'). 16 — это размер слоя. Каждый слой работает по следующей формуле: output = relu(dot(W, input) + b), где dot - скалярное произведение. Если задать размер слоя 16, тогда матрица весов W будет формы (input_dimension, 16).
Необходимо принять два архитектурных решения: 1) сколько всего слоёв использовать; 2) какой будет размер слоёв. Мы используем 3 слоя: 1 входной + 1 скрытый (размер 16, активация relu) и выходной слой с активацией sigmoid для получения выходной вероятности (число между 0 и 1):

Задание архитектуры сети:
from keras import models from keras import layers from keras import optimizers model = models.Sequential() model.add(layers.Dense(16, activation='relu', input_shape=(10000,))) model.add(layers.Dense(16, activation='relu')) model.add(layers.Dense(1, activation='sigmoid'))
Наконец, необходимо выбрать функцию потерь и оптимизатор. Поскольку перед нами стоит задача бинарной классификации и выходными данными сети является вероятность, хорошей идеей будет использовать бинарную кросс-энтропию binary_crossentropy в качестве функции потерь. К слову, это не единственный вариант. Можно использовать и, например, среднеквадратичную ошибку mean_squared_error. Но бинарная кросс-энтропия, как правило, наилучший вариант, если модель выводит вероятности. В качестве оптимизатора выберем среднеквадратичное распространение RMSProp. Мы так же будем следить за точностью во время обучения.
Компиляция модели:
from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
Чтобы следить за точностью модели во время обучения на данных, которые не участвовали в обучении, возьмём из исходной тренировочной выборки 10000 примеров для проверочной выборки:
x_val = x_train[:10000] partial_x_train = x_train[10000:] y_val = y_train[:10000] partial_y_train = y_train[10000:]
Теперь обучим модель на 20 итерациях подвыборками с размером 512. Следить за потерями и точностью будем с помощью проверочный выборки из 10000 примеров:
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
Python выведет в STDOUT примерно следующее:
Train on 15000 samples, validate on 10000 samples Epoch 1/20 15000/15000 [==============================] - 2s 132us/step - loss: 0.5213 - binary_accuracy: 0.7958 - val_loss: 0.4019 - val_binary_accuracy: 0.8541 Epoch 2/20 ... Epoch 19/20 15000/15000 [==============================] - 1s 99us/step - loss: 0.0091 - binary_accuracy: 0.9992 - val_loss: 0.6600 - val_binary_accuracy: 0.8670 Epoch 20/20 15000/15000 [==============================] - 1s 99us/step - loss: 0.0064 - binary_accuracy: 0.9996 - val_loss: 0.7630 - val_binary_accuracy: 0.8629
history — это объект, содержащий словарь history, в котором хранятся данные обо всём, произошедшем во время обучения:
>>> history_dict = history.history >>> history_dict.keys() dict_keys(['val_loss', 'val_binary_accuracy', 'loss', 'binary_accuracy'])
Нарисуем графики тренировочных и проверочных точности и потерь:
import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Потери при обучении')
plt.plot(epochs, val_loss_values, 'b', label='Потери при проверке')
plt.title('Потери при обучении и проверке', fontsize=18)
plt.xlabel('Итерации', fontsize=16)
plt.ylabel('Потери', fontsize=16)
plt.legend(fontsize=14)
plt.show()
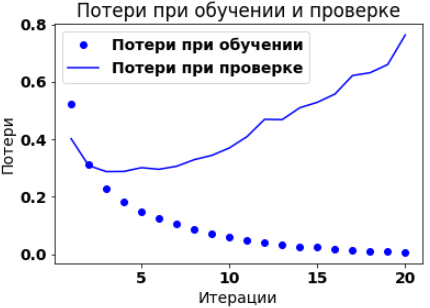
plt.clf()
acc_values = history_dict['binary_accuracy']
val_acc_values = history_dict['val_binary_accuracy']
plt.plot(epochs, acc, 'bo', label='Тренировочная точность')
plt.plot(epochs, val_acc, 'b', label='Проверочная точность')
plt.title('Тренировочная и проверочная точность')
plt.xlabel('Итерации')
plt.ylabel('Потери')
plt.legend()
plt.show()
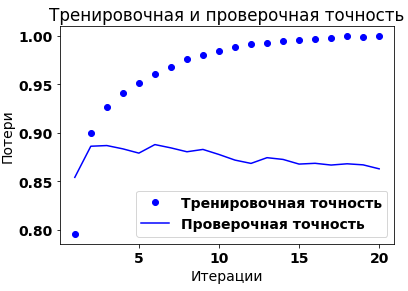
Как видно из графиков, тренировочные потери снижаются с каждой мтерацией, а тренировочная точность растёт. Для проверочной выборки пиковые значения приходятся на 4-ю итерации. Иными словами, модель показывает значительно лучшие результаты на тренировочной выборке, чем на проверочной, что говорит о переобучении. Один из вариантов предотвратить переобучение - это уменьшить количество итераций. В данном случае до трёх.
Теперь попробуем заново обучить сеть с нуля на четырёх итерациях и затем посмотреть результат на тестовых данных:
model = models.Sequential() model.add(layers.Dense(16, activation='relu', input_shape=(10000,))) model.add(layers.Dense(16, activation='relu')) model.add(layers.Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy',metrics=['accuracy']) model.fit(x_train, y_train, epochs=4, batch_size=512) results = model.evaluate(x_test, y_test) print (results)
Python выведет в STDOUT:
Epoch 1/4 25000/25000 [==============================] - 8s 319us/step - loss: 0.4577 - accuracy: 0.8116 Epoch 2/4 25000/25000 [==============================] - 2s 73us/step - loss: 0.2608 - accuracy: 0.9088 Epoch 3/4 25000/25000 [==============================] - 2s 73us/step - loss: 0.2026 - accuracy: 0.9281 Epoch 4/4 25000/25000 [==============================] - 2s 73us/step - loss: 0.1695 - accuracy: 0.9400 25000/25000 [==============================] - 4s 164us/step [0.30060292099952696, 0.8820000290870667]
Такой простой подход позволяет достичь точности 88%. Для использования обученной сети на практике (когда есть только входные данные, а ответ не известен):
model.predict(x_test)
array([[0.22884989],
[0.9998193 ],
[0.9301637 ],
...,
[0.11618775],
[0.11960122],
[0.72682405]], dtype=float32)



